[matlab正弦余弦函数图象]t=0:0.1:2*pi; >>y1=sin(t); >>y2=cos(t); >>plot(t,y2,'ro') >>close >>t=0:0.01:2*pi; >>y1=sin(t); >>y2=cos(t); >>plot(t,y2,'ro') >>hold on >>plot(t,y1) >>title('正...+阅读
这种函数,我没有一眼可以看出来的方法。你可以用几种特殊的情况定出函数图象大致样子。
1)函数的增长情况,单增单减等等。y=x为增函数,y=-1/x也未单增函数,所以两者之和也为增函数,但显然x不能为零。
2)明确了增减性,可以考虑x取值的几种特殊情况:
(1)x趋近于无穷小,显然-1/x趋近与负无穷大
(2)x趋近于无穷大,显然x为无穷大,-1/x为无穷小即接近为0,所以y接近正无穷大
(3)x从负向0逼近时,如x=-0.1与-0.01可以比较y的大小,知道y趋近正无穷大
(4)x从正向0逼近时,如x=0.1与0.01可以比较对应y的大小,知道y趋近负无穷大
(5)另外x其他特殊情况,x为1 -1 等等
其实前四条已经可以知道函数的图形。
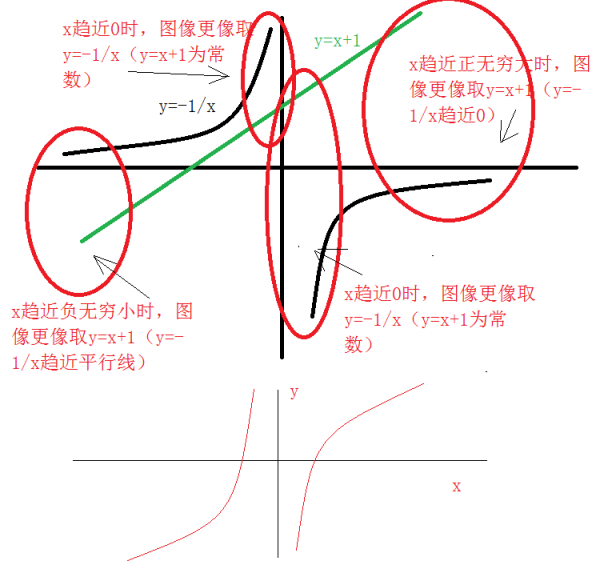
另外根据y=x+1和y=-1/x的图像进行叠加,可以比较方便的知道结果,见图:
函数及其图像
函数图象目录 函数图象的起源及意义 函数图象的定义 函数图象的形状 函数图象的作法 函数图象的作用 【读音】han shu [编辑本段]函数图象的起源及意义 函数观念古代早已有之,而函数概念则是由17世纪德国著名数学家莱布尼茨提出的。起初,人们研究函数,只是对着函数解析式反反复复地算来算去。后来,法国著名数学家笛卡儿引入了平面直角坐标系,该坐标系由两个数轴组成。两个数轴互相垂直,原点重合,单位长度相等。习惯上把铅直的数轴称为y轴,水平的数轴称为x轴,y轴的上方为正方向,x轴的右方为正方向。从此,平面上的每一个点都可以用平面直角坐标系的坐标表示。 直角坐标系引入后,人们发现,直角坐标系用有序数对表示点,而有序数对中的两个数恰恰可以用函数中的两个变量表示。
这是数学史上的伟大创举! 此后,人们就知道,函数可以通过坐标系转化成图形,从而直观地研究。数和形是数学的两大根基,以前毫不相干,正是坐标系的出现,把作为“数”的函数转化为作为“形”的图象,从此数学发展更蓬勃。令数有了几何意义,是很多高等数学的思想,如微积分中,导数的几何意义就是某函数的图象在一点上的切线的斜率。 [编辑本段]函数图象的定义 对于一个函数y=f(x),如果把其中的自变量x视为直角坐标系上的某一点的横坐标,把对应的唯一的函数值y视为此点的纵坐标,那么,这个函数y=f(x),无论x取何值,都同时确定了一个点,由于x的取值范围是无穷大,同样y也有无穷个,表示的点也就有无穷个。这些点在平面上组成的图形就是此函数的图象,简称图象。
[编辑本段]函数图象的形状 对于一个函数y=f(x),由x得到y并表示一个点,那么这无数个点在平面上是不是毫无规律呢?答案是否定的。实际上,函数的总类有很多,同一种函数的图象在人的直观上看来是相似的。例如,一次函数f(x)=kx+b的图象就是一条直线;而正比例函数f(x)=kx的图象,因为正比例函数是特殊的一次函数,所以其图象对于一次函数的图象来说也比较特殊,是一条过原点的直线;二次函数的图象是一条抛物线;反比例函数的图象是一组双曲线;正弦函数的图象称作正弦曲线,实际上是我们常说的波浪线,等等。 并非所有函数的图象都是无限长的直线或曲线。有些特殊的函数,其图象是一个点,而某些规定了自变量取值范围的函数,其图象则是一线段。 [编辑本段]函数图象的作法 我们知道了函数在坐标系上对应的每个点都是有规律的。
我们知道了一个函数的图象的基本形状,就可以很容易地作出这个函数的图象。 如对于正比例函数,我们只需代入一个x值得到y值,便确定了一个点,把这个点与原点连起来即可成功。因为正比例函数的图象是一根过原点的直线。而一次函数则需要多找一个点,把两个点连起来就可以,因为一次函数的图象是一根直线,两点确定一根直线。 非一次函数的图象比较麻烦,因为它们的图象是曲线。这时候,就要采用多点作图法。因为我们先前已经探讨过,每一种函数的图象在人的直观上都是相同的。比如作一个二次函数的图象,如果想精确些,我们就找10个点,因为二次函数的图象是一条抛物线,所以我们大致地按照抛物线的轨迹用平滑的曲线把它连起来。粗略些,可以找3个点,用平滑的曲线连起来,形状大致跟抛物线贴合即可。
[编辑本段]函数图象的作用 函数图象的出现是因为人们研究函数,从而渴望得到一种快捷方便的方式。所以函数图象的最大作用就是让人看到函数的变化,能更深入地研究。 再漂亮的函数解析式,也只不过是加减乘除开方平方、abcdefxyz和0123456789掺杂而成的枯燥算式。但把函数解析式表示成图象,我们能从中获取很多信息。如从函数的升降我们可以看出,某个函数的自变量在某个取值范围内令函数值增大还是减少;对于一个二元方程组,其中的每一个方程都可以看作是一个函数,对应一个图象,这些函数的图象的交点便是方程组的解;把一个方程看作一个函数,从其图象与数轴的交点存在或不存在、交点对应的坐标值可以知道此方程有解或无解,解是多少;对于一个由曲线组成的图形,可以放入直角坐标系,解出这些曲线的函数解析式,便可以用微积分计算出此图形的面积,这是初等数学无法做到的……以上所述不过是函数图象作用的凤毛麟角,而随着数学研究的深入,函数的应用也越来越广泛,而用图象研究函数是必然的。
函数是一门贴和实纪的学问所以我们要认真对待!
以下为关联文档:
画数学三角函数图像步骤直接先确定平衡位置,在确定振幅,然后列表取相邻的五个特殊点(三个平衡位置,两个最值点)画出一个周期内函数图象 直接画快,用sinx的图像变换太麻烦: sinx变化有两种方法 画sinx,然后y...
一次函数图象的画法精华提问1、一此函数的图像是一条直线,所以画一次函数图像就相当于画一条直线,所以只要确定两个点就可以确定一次函数的图像了。至于说这两个点如何选择,则可以结合具体的一次函数解析...
分式通分怎么做根据分数的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分。 把异分母分数分别化成与原来分数相等的同分母分数,叫做通分。 把甲数与乙数...
怎样用excel画函数图1、新建一个excel表格,双击打开。 2、在A1、 A2、A3、A4、A5、A6、A7、A8、A9、A10、A11、A12栏分别输入x、-5、-4、-3、-2、-1、0、1、2、3、4、5,B1栏输入y。 3、在B2栏...
怎么样用excel来画函数y 1x 1的图啊用Excel绘制函数图像 做教学工作的朋友们一定会遇到画函数曲线的问题吧!如果想快速准确地绘制一条函数曲线,可以借助EXCEL的图表功能,它能使你画的曲线既标准又漂亮。你一定会...
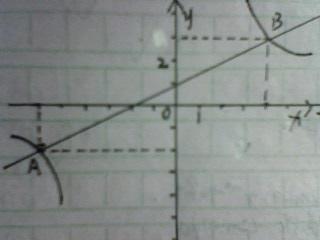
八年纪数学反比例函数图象???如图,一次函数Y=kx+b的图象与反比例函数Y=x分之m的图象相交于A、B两点. ⑴根据图象,分别写出A、B的坐标. ⑵求出两函数的解析式. ⑶根据图象回答:当x为何值时,一次函数的函数值...
如果一个类里面的构造函数的参数含有这个类的对象指针那怎么初不用担心,你这个问题不存在。 解决办法,让next = NULL,next想必你要表示的是链表的下一个,对吧,构造这一个的时候,下一个设置为NULL,是个不错的选择。 即使一定要构造,也不存在这个...
数学分式方程怎么解分式不等式解的方法其实都是一样的 第一步 先移项通分得: (2x+5)(2x-1)/(x+1)(2x-4)>0 第二步 分子除分母大于0说明分子、分母同号,因此可写为因式相乘的形式: (2x+5)(2x-1)(x+...
八年级下册数学分式这一章的整体思路可以更好的帮助学习分式的分式的概念:形如 ,其中分母B中含有字母,分数是整式而不是分式. 分式 中的字母代表什么数或式子是有条件的. (1)分式无意义时,分母中的字母 的取值使分母为零,即当B=0时分式无意义...