[计算机运算基础三补码的运算法则]法则 1 ：一个数的相反数的补码等于该数的补码的补码，即 [- X ] 补码 =[[ X ] 补码 ] 补码X = + 0000101（十进制 +5 ）-X = - 0000101（X的相反数，十进制 -5 ）[ X ] 补码 = 0000010...+阅读

运算法则是同底数幂相乘，底数不变，指数相加；同底数幂相除，底数不变，指数相减；幂的乘方，底数不变，指数相乘；积的乘方，等于每一个因式分别乘方。

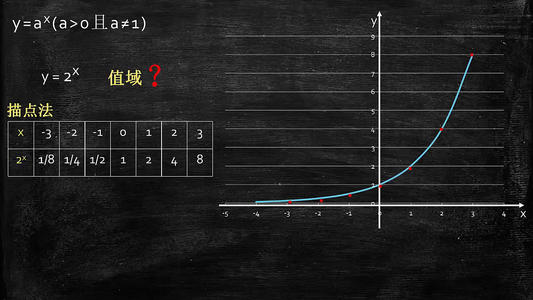
指数函数是重要的基本初等函数之一。一般地，指数函数定义域是R。对于一切指数函数来讲，值域为（0， +∞）。指数函数前系数为3，故不是指数函数。运算法则是同底数幂相乘，底数不变，指数相加；同底数幂相除，底数不变，指数相减；幂的乘方，底数不变，指数相乘；积的乘方，等于每一个因式分别乘方。

应用到值e上的这个函数写为exp(x)。还可以等价的写为ex，这里的e是数学常数，就是自然对数的底数，近似等于 2.718281828，还称为欧拉数。当a>1时，指数函数对于x的负数值非常平坦，对于x的正数值迅速攀升，在 x等于0的时候，y等于1。当0作为实数变量x的函数，它的图像总是正的（在x轴之上）并递增（从左向右看）。它永不触及x轴，尽管它可以无限程度地靠近x轴（所以，x轴是这个图像的水平渐近线。它的反函数是自然对数ln(x)，它定义在所有正数x上。

有时，尤其是在科学中，术语指数函数更一般性的用于形如（k属于R） 的函数，从上面关于幂函数的讨论就可以知道，要想使得x能够取整个实数集合为定义域，则只有使得a>0且a≠1。

指数怎么运算啊

一、对数的运算法则：

1、log(a) (M·N)=log(a) M+log(a) N

2、log(a) (M÷N)=log(a) M-log(a) N

3、log(a) M^n=nlog(a) M

4、log(a)b*log(b)a=1

5、log(a) b=log (c) b÷log (c) a

二、指数的运算法则：

1、[a^m]*[a^n]=a^(m+n)

2、[a^m]÷[a^n]=a^(m-n)

3、[a^m]^n=a^(mn)

4、[ab]^m=(a^m)*(a^m)

记忆口决：

有理数的指数幂，运算法则要记住。

指数加减底不变，同底数幂相乘除。

指数相乘底不变，幂的乘方要清楚。

积商乘方原指数，换底乘方再乘除。

非零数的零次幂，常值为 1不糊涂。

负整数的指数幂，指数转正求倒数。

看到分数指数幂，想到底数必非负。

乘方指数是分子，根指数要当分母。

扩展资料

指数的相关历史：

1607 年，利玛窦和徐光启合译欧几里得的 《几何原本》，在译本中徐光启重新使用了幂字，并有注解：“自乘之数曰幂。”这是第一次给幂这个概念下定义。

至十七世纪，具有“现代”意义的指数符号才出现。最初的，只是表示未知数之次数，但并无出现未知量符号。比尔吉则把罗马数字写于系数数字之上，以表示未知量次数。

其后，开普勒等亦采用了这符号。罗曼斯开始写出未知量的字母。1631 年，哈里奥特（ 1560-1621） 改进了韦达的记法，以 aa表示q^2 ， 以aaa 表示q^3。

1636 年，居于巴黎的苏格兰人休姆（ James Hume） 以小罗马数字放于字母之右上角的方式表达指数，该表示方式除了用的是罗马数字外，已与现在的指数表示法相同。笛卡儿（ 1596-1650） 以较小的印度阿拉伯数字放于右上角来表示指数，是现今通用的指数表示法。

8个指数运算公式

八个公式：

1、y=c(c为常数) y'=0;

2、y=x^n y'=nx^(n-1);

3、y=a^x y'=a^xlna y=e^x y'=e^x;

4、y=logax y'=logae/x y=lnx y'=1/x ;

5、y=sinx y'=cosx;

6、y=cosx y'=-sinx;

7、y=tanx y'=1/cos^2x;

8、y=cotx y'=-1/sin^2x。 运算法则：加（减）法则：[f(x)+g(x)]'=f(x)'+g(x)'乘法法则：[f(x)*g(x)]'=f(x)'*g(x)+g(x)'*f(x)除法法则：[f(x)/g(x)]'=[f(x)'*g(x)-g(x)'*f(x)]/g(x)^2在某种情况下（基数>0，且不为1），指数运算中的指数可以通过对数运算求解得到。 幂（n^m）中的n，或者对数（x=logaN）中的 a(a>0且a不等于1)。在指数函数的定义表达式中，在a^x前的系数必须是数1，自变量x必须在指数的位置上，且不能是x的其他表达式，否则，就不是指数函数。 当a>1时，指数函数对于x的负数值非常平坦，对于x的正数值迅速攀升，在 x等于0的时候，y等于1。当0 全部

指数如何运算？

指数的运算法则：

1、[a^m]*[a^n]=a^(m+n) 【同底数幂相乘，底数不变，指数相加】

2、[a^m]÷[a^n]=a^(m-n) 【同底数幂相除，底数不变，指数相减】

3、[a^m]^n=a^(mn) 【幂的乘方，底数不变，指数相乘】

4、[ab]^m=(a^m)*(a^m) 【积的乘方，等于各个因式分别乘方，再把所得的幂相乘】

扩展资料

同底数幂的除法是整式除法的基础，要熟练掌握。同底数幂的除法法则是根据除法是乘法的逆运算归纳总结出来的，和前面讲的幂的运算的三个法则相比，在这里底数a是不能为零的，否则除数为零，除法就没有意义了。

又因为在这里没有引入负指数和零指数，所以又规定m>n。能从特殊到一般地归纳出同底数幂的除法法则。

以下为关联文档：

指数函数是什么指数函数的一般形式为y=a^x(a>0且不=1) ，从上面我们对于幂函数的讨论就可以知道，要想使得x能够取整个实数集合为定义域，则只有使得 如图所示为a的不同大小影响函数图形的情况。...

数学对数函数的运算对数的运算法则及变式法则答：若a^b=C,(a>0,a≠1)，则b=log(a)C.把b=log(a)C代回去，便得a^log(a)C=C.（此式很有用）log(a)MN=log(a)M+log(a)Nlog(a)(M/N)=log(a)M-log(a)Nlog(a)(M^n...

高中数学之对数函数的运算对数函数运算法则 本站 悬赏分：0 | 提问者：匿名 | 解决时间：211-10 11:55 | 检举 最佳答案 对数的运算法则及变式法则 答：若a^b=C,(a>0,a≠1)，则b=log(a)C. 把b=log(a)C代回去，便...

幂函数的基本运算有哪些1、同底数幂的乘法： 2、幂的乘方（a^m）^n=a^(mn)，与积的乘方（ab）^n=a^nb^n。 3、同底数幂的除法： (1)同底数幂的除法：am÷an=a(m-n) (a≠0, m, n均为正整数，并且m>n)。 (2)零指数：a0=1...

数学中指数函数对数函数幂函数的运算法则当指数x是正整数n时，a^n叫做正整数指数幂. 当指数x是0，且a不等于0时，a^0叫做零指数幂. 当指数x是负整数-n，且a不等于0时，a^-n叫做负整数指数幂. 以上各种幂统称为整数指数幂 整数...

数学问题什么是函数还有正弦函数余弦函数又是什么.正弦、余弦的概念是本章的起点，同时又是重点、关键.这是本章知识的基础. 在直角三角形ABC中，当一个锐角（∠A）取固定值时，它的直角边与斜边的比值也是一个固定值. ,cos= . 实际上...

刺猬法则是什么刺猬法则刺猬法则强调的就是人际交往中的“心理距离效应”。运用到管理实践中，就是领导者如要搞好工作，应该与下属保持亲密关系，但这是“亲密有间”的关系，是一种不远不近的恰当...

数学复数的除法运算法则加法运算法则数学复数的除法运算法则加法运算法则，复数的运算法则：复数的加法运算 复数的加法按照以下规定的法则进行：设z1=a+bi,z2=c+di是任意两个复数， 则它们的和是 （a+bi）+(c+di)=(a+c)+(b...

整式的运算法则整式的运算法则，运算定律公式：一、整式 1.单项式 ①由数与字母的乘积组成的代数式叫做单项式。单独一个数或字母也是单项式。 ②单项式的系数是这个单项式的数字因数，作为单项...