[初中三角函数的基本公式]1.诱导公式 sin(-a)=-sin(a) cos(-a)=cos(a) sin(π2-a)=cos(a) cos(π2-a)=sin(a) sin(π2+a)=cos(a) cos(π2+a)=-sin(a) sin(π-a)=sin(a) cos(π-a)=-cos(a) sin(π+a)=-sin(a) cos(π+...+阅读
tanA=sinA/ cos A
tanA=1/cotA
(sinA)^2+( cos A)^2=1
正弦定理
a/sinA=b/sinB=c/sinC
余弦定理
a^2=b^2+c^2-2bc*cosA b^2=c^2+a^2-2ac*cosB c^2=a^2+b^2-2ab*cosC (1)二倍角公式: (a)sin2a=2*sina*cosa (b)cos2a=cosa^2-sina^2=2cosa^2-1=1-2sina^2 (c)tan2a= 2tana/(1-tana^2) (2)以正切表示二倍角 (a)sin2a= 2tana/(1+tana^2) (b)cos2a= (1-tana^2)/(1+tana^2) (c) tan2a= 2tana/(1-tana^2) (3)三倍角公式 (a)sin3a=3sina -4sina^3 (b)cos3a=4cosa^3 -3cosa1、积化和差公式: sinαsinβ=-1/2[cos(α+β)-cos(α-β)] cosαcosβ=1/2[cos(α+β)+cos(α-β)] sinαcosβ=1/2[sin(α+β)+sin(α-β)] cosαsinβ=1/2[sin(α+β)-sin(α-β)] 2、和差化积公式 sinθ+sinφ=2sin[(θ+φ)/2]cos[(φ-θ)/2] sinθ-sinφ=2cos[(θ+φ)/2]sin[(φ-θ)/2] cosθ+cosφ=2cos[(θ+φ)/2]sin[(φ-θ)/2] cosθ-cosφ=-2sin[(θ+φ)/2]sin[(θ-φ)/2]
跪求所有三角函数转换关系以及对数函数关系式
同角三角函数的基本关系式 倒数关系: 商的关系: 平方关系:tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα sin2α+cos2α=1 1+tan2α=sec2α 1+cot2α=csc2α 诱导公式sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα cot(2kπ+α)=cotα (其中k∈Z) 两角和与差的三角函数公式 万能公式 sin(α+β)=sinαcosβ+cosαsinβ sin(α-β)=sinαcosβ-cosαsinβ cos(α+β)=cosαcosβ-sinαsinβ cos(α-β)=cosαcosβ+sinαsinβ tanα+tanβ tan(α+β)=—————— 1-tanα ·tanβ tanα-tanβ tan(α-β)=—————— 1+tanα ·tanβ 2tan(α/2) sinα=—————— 1+tan2(α/2) 1-tan2(α/2) cosα=—————— 1+tan2(α/2) 2tan(α/2) tanα=—————— 1-tan2(α/2) 半角的正弦、余弦和正切公式 三角函数的降幂公式 二倍角的正弦、余弦和正切公式 三倍角的正弦、余弦和正切公式 sin2α=2sinαcosα cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α 2tanα tan2α=————— 1-tan2α sin3α=3sinα-4sin3α cos3α=4cos3α-3cosα 3tanα-tan3α tan3α=—————— 1-3tan2α 三角函数的和差化积公式 三角函数的积化和差公式 α+β α-β sinα+sinβ=2sin—--·cos—-— 2 2 α+β α-β sinα-sinβ=2cos—--·sin—-— 2 2 α+β α-β cosα+cosβ=2cos—--·cos—-— 2 2 α+β α-β cosα-cosβ=-2sin—--·sin—-— 2 2 1 sinα ·cosβ=-[sin(α+β)+sin(α-β)] 2 1 cosα ·sinβ=-[sin(α+β)-sin(α-β)] 2 1 cosα ·cosβ=-[cos(α+β)+cos(α-β)] 2 1 sinα ·sinβ=- -[cos(α+β)-cos(α-β)] 2 化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式) 倒数关系: 商的关系: 平方关系:tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα sin2α+cos2α=1 1+tan2α=sec2α 1+cot2α=csc2α
三角函数sin cos tan之间的转换公式
正弦定理:
a/sina=b/sinb=c/sinc。
余弦定理:
a^2=b^2+c^2-2bc*cosa。
b^2=c^2+a^2-2ac*cosb。
c^2=a^2+b^2-2ab*cosc。
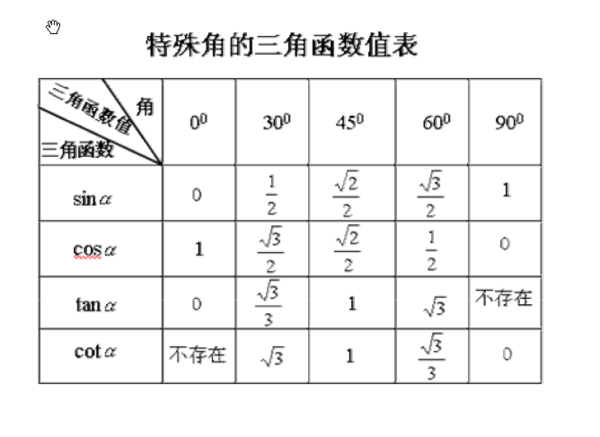
三角函数主要运用方法:
三角函数以角度(数学上最常用弧度制,下同)为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。也可以等价地用与单位圆有关的各种线段的长度来定义。
三角学中”正弦”和”余弦”的概念就是由印度数学家首先引进的,他们还造出了比托勒密更精确的正弦表。
托勒密和希帕克造出的弦表是圆的全弦表,它是把圆弧同弧所夹的弦对应起来的。印度数学家不同,他们把半弦(AC)与全弦所对弧的一半(AD)相对应,即将AC与∠AOC对应,这样,他们造出的就不再是”全弦表”,而是”正弦表”了。
以下为关联文档:
初中三角函数公式表sin是 对边比斜边 ,cos是邻边比斜边,tan是对边比邻边 cot邻边比对边。 sin30是二分之一,45是二分之根二,60是二分之根三。cos304560分别是二分之根三,二分之根二,二分之一。 tan30...

高分关于锐角三角函数sin(A+B)=sinAcosB+cosAsinBnbsp;---amp;gt;sin2A=2sinAcosAnbsp;cos(A+B)=cosAcosB-sinAsinBnbsp;---amp;gt;cos2A=(cosA)^2-(sinA)^2=(1-(sinA)^2-(sinA)^2=1-2(sinA)^2=2...
数学锐角三角函数初学锐角三角函数时我们最好借助画直角三角形来理解。 1,Sin α 指的是构成直角的两条边中的某一条与斜边够成的角的正弦直 算法是 构成直角的两条边中的某一条与斜边够成的...
求初三三角函数知识在一个直角三角形中,正弦: ∠A的对边sinA=—————— 斜边锐角的正弦值随着角度的增大而增大。sin0°=0 根号2sin45°=----- sin90°=1 2sin30°=2分之1sin60°=2分之根号3...
函数的极限怎么求啊极限可以说是数学分析的基础,对于高等数学的整体学习理解都是十分重要的。因此这一块的内容一定要好好掌握。对于这一方面的内容给你以下几点建议方便理解: 1>;掌握好ε-δ(或...

利用函数极限求数列极限例题请解析为什么x趋近于正无穷?这一步是怎么变化来的? 因为n为正整数,趋于+∞,通过求函数的极限求数列的极限是利用收敛函数的子列必收敛,且极限相同。 lntan(π/4+2/x)= ln(1+tan(π/4+2/x)-1...
利用函数极限求数列极限例题你写的好乱,看了半天看懂了 第一个等号:(tanx/x)^((1/(x^2))=e^(ln (tanx/x)/(x^2)),其中取极限穿越进指数 第二个等号:利用了当x为无穷小量时 ln(x+1)同阶于x 第三个等号:指数中的...
初中的三角函数公式sin(A+B)=sinAcosB+cosAsinB --->sin2A=2sinAcosA cos(A+B)=cosAcosB-sinAsinB --->cos2A=(cosA)^2-(sinA)^2=(1-(sinA)^2-(sinA)^2=1-2(sinA)^2=2(cosA)^2-1. tan(A+B)=(ta...
初中三角函数所有公式倒数关系: 商的关系: 平方关系: tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα sin2α+cos2α=1 1+tan2α=...



