[解方程数学问题教程]1、6x²-13x-5=0 (2x-5)(3x 1)=0 2x-5=0或3x 1=0 x=5/2或x=-1/3 2、x² 2x-2=0 x² 2x 1=3 (x 1)²=3 x 1=±√3 x=±√3-1 3、2y² 8y-1=0 y² 4y-1/2=0 y² 4y 4-4-1/2=0...+阅读
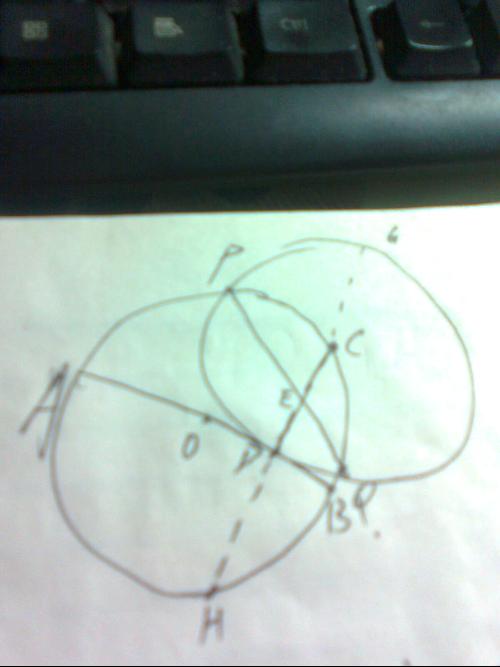
设Q(s,t),M(x,y)。
显然:s^2+t^2=1
因为A,M,Q三点共线,则:
(y-t)/(x-s)=(t-0)/(s-2)
(y-t)(s-2)=t(x-s).........(1)
又因为角AOQ的平分线交AQ于点M
所以:cos向量OM与向量OA的夹角=cos向量OM与向量OQ的夹角
故:向量OM*向量OA/(|OM|*|OA|)=向量OM*向量OQ/(|OM*|OQ|)
2x/2=sx+ty
(s-1)x+ty=0.......(2)
联立(1),(2)可解得:
s=(2x-x^2)/(2x-x^2-y^2)
t=xy/(2x-x^2-y^2)
将s,t代入圆方程x^2+y^2=1,得:
(2x-x^2)^2+x^2y^2=(2x-x^2-y^2)^2
(2x-x^2)^2+x^2y^2=(2x-x^2)^2-4xy^2+2x^2y^2+y^4
y^4+x^2y^2-4xy^2=0
y^2=-x^2+4x
即:(x-2)^2+y^2=4
这就是M的轨迹方程,它是圆心在(2,0),半径为2的圆。
数学关于圆的方程的知识
如果是相切的话,且λ= -1,那就表示过切点切与两圆相切的直线,首先方程化简后为直线方程的形式。因为λ= -1时切点是该方程的解,并且除切点外的任一圆上一点都不是该方程的解(除切点外的点只能满足一个式子为零另一个必不为零)。 如果λ≠-1首先方程化简后肯定是个圆方程的形式,而且切点也必为其解所以该圆必过切点,所以应该是过切点的圆系。
照此讨论下去,当两圆相离时,没有公共解。但是当λ= -1,λ≠-1时,方程的解任然是直线和圆。从代数上说的话,设f1=x²+y²+D1 x+E1y+F1 f2=λ(x²+y²+D2x+E2y+F2) 那么方程的解就是满足f1=f2的解但是很明显不可能存在使 f1,f2同时为零的解,也就是说。这个方程的解和这两个圆没关系了。
以下为关联文档:
2道数学解方程1、x²-(x-5)(x-8)=220 x²-(x²-8x-5x+40)=220 x²-x²+8x+5x-40=220 13x=260 x=20 2、80+30+20%x=60%(100+30+x) 80+30+0.2x=0.6(100+30+x) 110+0.2x=60+18+0.6x 0.6x-0.2x=11...
圆与圆的位置关系 解:延长CD交圆O于H,延长DC交圆C于G 因为CD⊥AB于D 所以,DH=CD(垂径定理) 即CH=2CD 因为CD^2=AD*BD(如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。) 且AD...
数学中的方程和方程组问题1. 设分子为x,分母为y。则: x+y=122 (1) (x-19)/(y-19)=1/5 (2) 由 (2)得:5x-95=y-19 (3) 由 (1)和 (3)得:x=33, y=89 2. 设从B堆中拿到A堆黑子x个,白子y个。 A堆中白子占50%(白子个数等...
数学方程实际应用(1) 当是10万时,全部出租。这时为13万。(13000-10000)/5000=6 30-6=24间 (2)设租金为x万. 那么能租出的店铺:30-[(x-10万)/5000] 即先不考虑付出,盈利为:1万*30-[(x-10万)/5000]...
数学的直线方程问题x+y-1=0,3x-y+4=0不平行,故是平行四边形的邻边交点是(-3/4,7/4),则这一点是平行四边形的一个顶点。它的对角线的交点是M(3,3)因为平行四边形的对角线互相平分,所以M是两个相对的...
数学分式方程怎么解分式不等式解的方法其实都是一样的 第一步 先移项通分得: (2x+5)(2x-1)/(x+1)(2x-4)>0 第二步 分子除分母大于0说明分子、分母同号,因此可写为因式相乘的形式: (2x+5)(2x-1)(x+...
数学回归方程公式y=bx+a 回归分析 regression analysis 回归分析是处理多变量间相关关系的一种数学方法。相关关系不同于函数关系,后者反映变量间的严格依存性,而前者则表现出一定程度的波动性...
求数学分式方程解法分式方程的解法: :①去分母(方程两边同时乘以最简公分母,将分式方程化为整式方程) ;②按解整式方程的步骤(移项,合并同类项,系数化为1)求出未知数的值 ;③验根(求出未知数的值后必须验根...
数学积分求解数学物理方程分享一种解法,应用“正态分布密度函数的性质”求解。∵X~N(μ,δ²),则其密度函数f(x)=Ae^[-(x-μ)²/(2δ²)]。其中A=1/[δ√(2π)], 有∫(-∞.∞)f(x)dx=1、∫(-∞.∞)xf(x)dx=E(x)=μ...