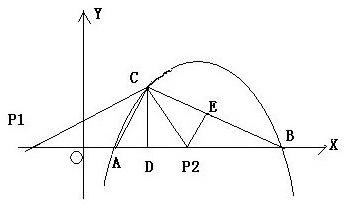
[数学压轴题如图抛物线Y AX2 BX c经过原点O与X轴交于另](1):先由C(2.2)推出 一次函数 然后把B X值 代入 即可求出B 的坐标 然后设2次函数为Y=ax^2+bx 因为该与Y轴 交点为0 代入 B C 数值 求出 (2) 分析 什么时候面积最大 已ON为底...+阅读
在《几何学》(是《方法论》中的一部分)卷一中,他用平面上的一点到两条固定直线的距离来确定点的距离,用坐标来描述空间上的点。他进而创立了解析几何学,表明了几何问题不仅可以归结成为代数形式,而且可以通过代数变换来实现发现几何性质,证明几何性质。
笛卡尔把几何问题化成代数问题,提出了几何问题的统一作图法。为此,他引入了单位线段,以及线段的加、减、乘、除、开方等概念,从而把线段与数量联系起来,通过线段之间的关系,“找出两种方式表达同一个量,这将构成一个方程”,然后根据方程的解所表示的线段间的关系作图。
在卷二中,笛卡儿用这种新方法解决帕普斯问题时,在平面上以一条直线为基线,为它规定一个起点,又选定与之相交的另一条直线,它们分别相当于x轴、原点、y轴,构成一个斜坐标系。那么该平面上任一点的位置都可以用(x,y)惟一地确定。帕普斯问题就化成了一个含两个未知数的二次不定方程。笛卡儿指出,方程的次数与坐标系的选择无关,因此可以根据方程的次数将曲线分类。
《几何学》一书提出了解析几何学的主要思想和方法,标志着解析几何学的诞生。此后,人类进入变量数学阶段。
在卷三中,笛卡尔指出,方程可能有和它的次数一样多的根,还提出了著名的笛卡尔符号法则:方程正根的最多个数等于其系数变号的次数;其负根的最多个数(他称为假根)等于符号不变的次数。笛卡尔还改进了韦达创造的符号系统,用a,b,c,…表示已知量,用x,y,z,…表示未知量。
解析几何的出现,改变了自古希腊以来代数和几何分离的趋向,把相互对立着的“数”与“形”统一了起来,使几何曲线与代数方程相结合。笛卡儿的这一天才创见,更为微积分的创立奠定了基础,从而开拓了变量数学的广阔领域。
正如恩格斯所说:“数学中的转折点是笛卡尔的变数。有了变数,运动进入了数学,有了变数,辩证法进入了数学,有了变数,微分和积分也就立刻成为必要了。”
[编辑本段]影响及评价
笛卡尔在哲学上是二元论者,并把上帝看作造物主。但笛卡尔在自然科学范围内却是一个机械论者,这在当时是有进步意义的。
笛卡尔是欧洲近代哲学的奠基人之一,黑格尔称他为“现代哲学之父”。他自成体系,熔唯物主义与唯心主义于一炉,在哲学史上产生了深远的影响。
笛卡尔的方法论对于后来物理学的发展有重要的影响。他在古代演绎方法的基础上创立了一种以数学为基础的演绎法:以唯理论为根据,从自明的直观公理出发,运用数学的逻辑演绎,推出结论。这种方法和培根所提倡的实验归纳法结合起来,经过惠更斯和牛顿等人的综合运用,成为物理学特别是理论物理学的重要方法。作为他的普遍方法的一个最成功的例子,是笛卡尔运用代数的方法的来解决几何问题,确立了坐标几何学即解析几何学的基础。
笛卡尔的方法论中还有两点值得注意。第一,他善于运用直观“模型”来说明物理现象。例如利用“网球”模型说明光的折射;用“盲人的手杖”来形象地比喻光信息沿物质作瞬时传输;用盛水的玻璃球来模拟并成功地解释了虹霓现象等。第二,他提倡运用假设和假说的方法,如宇宙结构论中的旋涡说。此外他还提出“普遍怀疑”原则。这一原则在当时的历史条件下对于反对教会统治、反对崇尚权威、提倡理性、提倡科学起过很大作用 。
以下为关联文档:
抛物线yax2十bx十c顶点20 16这个二次函数的解析式是1.把y=-1/4x*2+1/2x-1化成y=a(x-h)*2+k的形式,并指出图像的开口方向,对称轴和顶点坐标2.已知二次函数y=ax*2+bx+c,当x=4时y=3;当x=-1时y=-8;当x=2时y=1求这个二次函数的解析式3....
抛物线所有公式一般式:y=aX2+bX+c(a、b、c为常数,a≠0) 顶点式:y=a(X-h)2+k(a、h、k为常数,a≠0) 交点式(两根式):y=a(x-x1)(x-x2) (a≠0) 其中抛物线y=aX2+bX+c(a、b、c为常数,a≠0)与x轴交点坐标...
数学抛物线顶点坐标公式法怎么求公式法即记住公式,y=ax²+bx+c顶点坐标为( -b/(2a),(4ac-b²)/(4a)) 如:求y=-3x²-x+1的顶点, 即 a=-3,b=-1,c=1 -b/(2a)=1/(-6)=-1/6 (4ac-b²)/(4a)=(-12-1)/(-12)=13/12 所以顶点...
抛物线如何计算平面内,到定点与定直线的距离相等的点的轨迹叫做抛物线。其中定点叫抛物线的焦点,定直线叫抛物线的准线。抛物线是指平面内到一个定点F(焦点)和一条定直线l(准线)距离相等的点的轨...
谁能告诉我椭圆双曲线抛物线焦点分别在x轴y轴的参数方程啊椭圆方程x^2/a^2+y^2/b^2=1 参数方程 x=acosθ y=bsinθ 焦点在x轴上 y^2/a^2+x^2/b^2=1 参数方程 y=acosθ x=bsinθ 焦点在y轴上 双曲线x^2/a^2-y^2/b^2=1 参数方程 x=ase...
加工中心编写抛物线用宏程序怎么编是数控铣吧。 弧线是有点一点一点形成的,你可以用看图软件打开看看他的特点 就像下面的图你把每一行最右边的点连在一起你就发现他就是个弧。则你反过来弄你就成了也就是要用...
初三数学抛物线(1)令y=ax²—8ax+12a=0,求得两根分别是2,6 所以A点B点的坐标分别是(2,0),(6,0) 又知道△OCA∽△OBC 所以OC:OB=OA:OC,即OC²=OA*OB=2*6=12,所以OC=√12=2√3 (2)要求抛物线函数...
初三数学关于抛物线的(1)由抛物线表达式得到C点坐标(0,-3),与(1,m)距离根号5,解得m=-1或-5。因为ABC在圆上,所以m>-3,得到m=-1。设AB坐标为(x,0),由半径根号5,圆心(1,-1)得到AB分别是(-1,0),(3,0)。代入抛物线表...
切线理论如何实战应用实战运用 下面,我们就介绍利用趋线判断短期、中期和长期买入时机的方法。 1、短期下降趋线向上突破是短线买入时机 在中期下跌趋势中,股价主要以下跌为主,高点和低点都不断下移...



