[excel中怎么用函数计算年龄和工龄求具体步骤]假设A1是出生日期或者入职日期,B1用公式 =INT(DAYS360(A1,NOW())/360)&;"年"&INT((DAYS360(A1,NOW())/360-INT(DAYS360(A1,NOW())/360))*360/30)&;"月"&ROUNDUP((DAYS360(A1,...+阅读
初中数学锐角三角函数通常作为选择题,填空题和应用题压轴题出现,考察同学们灵活运用公式和定理能力,是中考一大难点之一。初中数学锐角三角函数知识点一览:锐角三角函数定义,正弦(sin),余弦(cos)和正切(tan)介绍,锐角三角函数公式(特殊三角度数的特殊值,两角和公式半角公式,和差化积公式),锐角三角函数图像和性质,锐角三角函数综合应用题。
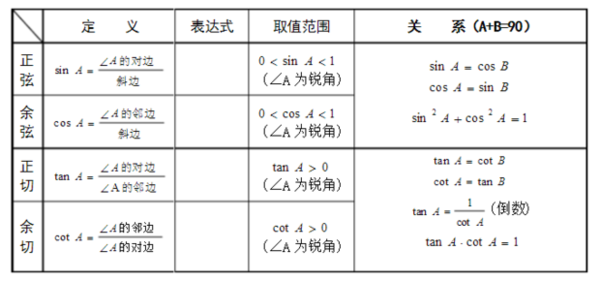
一、锐角三角函数定义 锐角三角函数是以锐角为自变量,以此值为函数值的函数。如图:我们把锐角∠A的正弦、余弦、正切和余切都叫做∠A的锐角函数。 锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。初中数学主要考察正弦(sin),余弦(cos)和正切(tan)。 正弦(sin)等于对边比斜边;sinA=a/c 余弦(cos)等于邻边比斜边;cosA=b/c 正切(tan)等于对边比邻边;tanA=a/b 余切(cot)等于邻边比对边;cotA=b/a
二、锐角三角函数公式 关于初中三角函数公式,在考试中用的最多的就是特殊三角度数的特殊值。如: sin30°=1/2 sin45°=√2/2 sin60°=√3/2 cos30°=√3/2 cos45°=√2/2 cos60°=1/2 tan30°=√3/3 tan45°=1 tan60°=√3[1] cot30°=√3 cot45°=1 cot60°=√3/3 其次就是两角和公式,这是在初中数学考试中问答题中容易用到的三角函数公式。两角和公式 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA) 除了以上常考的初中三角函数公示之外,还有半角公式和和差化积公式也在选择题中用到。所以同学们还是要好好掌握。 半角公式 sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2) cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2) tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA)) ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA)) 和差化积 2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B) 2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B) sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgBsin(A+B)/sinAsinB - ctgA+ctgBsin(A+B)/sinAsinB
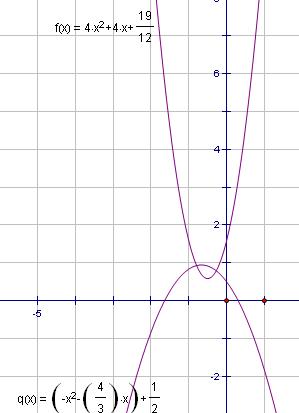
三、锐角三角函数图像和性质
四、锐角三角函数综合应用题 已知:一次函数y=-2x+10的图象与反比例函数y=k/x(k>0)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在
(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,-2a+10),B(b,-2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若BC/BD=5/2,求△ABC的面积. 考点: 反比例函数综合题;待定系数法求一次函数解析式;反比例函数与一次函数的交点问题;相似三角形的判定与性质. 解答: 解:
(1)把A(4,2)代入y=k/x,得k=4*2=8. ∴反比例函数的解析式为y=8/x. 解方程组y=2x+10 y=8/x,得x=1 y=8 或x=4 y=2, ∴点B的坐标为(1,8); (2)①若∠BAP=90°, 过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1, 对于y=-2x+10, 当y=0时,-2x+10=0,解得x=5, ∴点E(5,0),OE=5. ∵A(4,2),∴OH=4,AH=2, ∴HE=5-4=1. ∵AH⊥OE,∴∠AHM=∠AHE=90°. 又∵∠BAP=90°, ∴∠AME+∠AEM=90°,∠AME+∠MAH=90°, ∴∠MAH=∠AEM, ∴△AHM∽△EHA, ∴AH/EH=MH/AH, ∴2/1=MH/2, ∴MH=4, ∴M(0,0), 可设直线AP的解析式为y=mx 则有4m=2,解得m=1/2, ∴直线AP的解析式为y=1/2x, 解方程组y=1/2x, y=8/x,得x=4 y=2 或x=?4 y=?2, ∴点P的坐标为(-4,-2). ②若∠ABP=90°, 同理可得:点P的坐标为(-16,-1/2). 综上所述:符合条件的点P的坐标为(-4,-2)、(-16,-1/2); (3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2, 则有BS∥CT,∴△CTD∽△BSD, ∴CD/BD=CT/BS. ∵BC/BD=5/2, ∴CT/BS=CD/BD=3/2. ∵A(a,-2a+10),B(b,-2b+10), ∴C(-a,2a-10),CT=a,BS=b, ∴a/b=3/2 ,即b=2/3a. ∵A(a,-2a+10),B(b,-2b+10)都在反比例函数y=k/x的图象上, ∴a(-2a+10)=b(-2b+10), ∴a(-2a+10)=2/3 a(-2*2/3a+10). ∵a≠0, ∴-2a+10=2/3 (-2*2/3a+10), 解得:a=3. ∴A(3,4),B(2,6),C(-3,-4). 设直线BC的解析式为y=px+q, 则有2p+q=6 ?3p+q=?4, 解得:p=2q=2, ∴直线BC的解析式为y=2x+2. 当x=0时,y=2,则点D(0,2),OD=2, ∴S△COB=S△ODC+S△ODB=1/2 ODCT+1/2ODBS=1/2*2*3+1/2*2*2=5. ∵OA=OC, ∴S△AOB=S△COB, ∴S△ABC=2S△COB=10. 以上就是初中数学锐角三角函数知识点总结,小编推荐同学继续浏览《初中数学知识点专题汇总》。对于想要通过参加初中数学补习班来获得优质的数学学习资源和学习技巧,使自身成...
以下为关联文档:
小学数学知识点总结全部小学数学一年级(上):1. 数一数2. 比一比 (多少,长短,高矮)3. 1-5的认识与加减法(读写,顺序,大小比较)4. 认识图形和物体 (标准图形的直观认识)5. 分类6. 6-10的认识和加减 (读写,顺序,大小比...
初中数学2次函数1解: 二次函数y=-x²+ax+b-b²的顶点式为: [a/2,(4b-4b²+a²)/4] 带入二次函数y=4x²+4x+19/12中,得: 4(a/2)²+4(a/2)+19/12=(4b-4b²+a²)/4 9a²+24a+12b²-12b+19=0 (3a+4)...
初中物理热学知识点总结公式1. 温度:是指物体的冷热程度。 2. 温度计使用: (1)使用前应观察它的量程和最小刻度值; (2)使用时温度计玻璃泡要全部浸入被测液体中,不要碰到容器底或容器壁; (3)待温度计示数稳定后再...
小学信息技术知识点一(上): 1、 电脑的用途;电脑硬件(主机、显示器、键盘、鼠标)。 2、 开启电脑;热启动;电脑软件;关闭电脑。知识窗:认识桌面。 3、 打开记事本;双击鼠标左键;拖动鼠标;移动记事本;关闭记事...
初中高效过滤器的各项知识点空调净化系统中初中高效过滤的简单介绍 1、什么叫有、无隔板高效过滤器的实际尺寸和名义尺寸? 有无隔板高效过滤器为什么有实际尺寸和名义尺寸之分,是因为名义尺寸是包括外框...
高分关于锐角三角函数sin(A+B)=sinAcosB+cosAsinBnbsp;---amp;gt;sin2A=2sinAcosAnbsp;cos(A+B)=cosAcosB-sinAsinBnbsp;---amp;gt;cos2A=(cosA)^2-(sinA)^2=(1-(sinA)^2-(sinA)^2=1-2(sinA)^2=2...
数学锐角三角函数初学锐角三角函数时我们最好借助画直角三角形来理解。 1,Sin α 指的是构成直角的两条边中的某一条与斜边够成的角的正弦直 算法是 构成直角的两条边中的某一条与斜边够成的...
初中三角函数知识点1、勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方。 2、在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B) 3、任意锐角的正弦值等于它的余角的余弦值;任意...
我想知道关于初中数学的三角函数的知识初中部分三角函数的简介 基本初等内容 它有六种基本函数(初等基本表示): 函数名 正弦 余弦 正切 余切 正割 余割 正弦函数 sinθ=y/r 余弦函数 cosθ=x/r 正切函数 tanθ=y/x...