[初中反证法例题]在△ABC中，D、E分别是AB、AC上的任意两点，用反证法证明，BE与AC不能互相平分。假设BE与AC可以平分 两条相互平分的线段的端点间可以做出一个平行四边形，这应该知道吧 你先做出一...+阅读

∵a∥b,a不平行c

∴b不平行c 你这个推倒已经把结果带进去了·~

已知：A∥B,B∥C,

求证：A∥C

证明：∵A∥B,B∥C（已知）

∴∠1=∠2，∠2=∠3（两直线平行，同位角相等）

∴∠1=∠3（等量代换）

∴A∥C（同位角相等，两直线平行）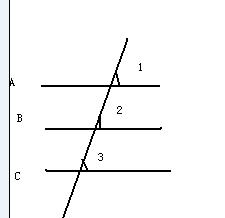

以下为关联文档：

初二反证法的题目抱歉，刚才没看到反证法~~ 已知：如图，AB∥EF,CD∥EF 求证：AB∥CD 假设AB与CD不平行，则AB与CD相交， 设交点为P。 P在AB上，EF外， 又∵AB∥EF,CD∥EF, 这与平行线基本性质相矛盾， ∴AB∥C...

初二数学题目反证法假设x、y、z全小于等于零 则x+y+z=a2-bc+b2-ca+c2-ab小于等于零 而2(x+y+z) =c2-2bc+b2+b2-2ab+a2+a2-2ca+c2 =(c-b)2+(b-a)2+(a-c)2 是大于等于零的 这样的话，x+y+z只能等于...