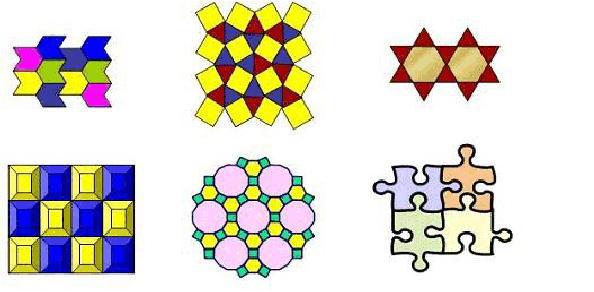
用形状、大小完全相同的几种或几十种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的密铺，又称做平面图形的镶嵌。

可单独密铺的图形

1、任意三角形、任意凸四边形都可以密铺。

2、正三角形、正四边形、正六边形可以单独用于平移密铺。

3、三对对应边平行的六边形可以单独密铺。

4、目前仅发现十五类五边形能密铺。

密铺的历史背景：

1619 年 —— 数学家奇柏（ J.Kepler ）第一个利用正多边形

铺嵌平面。

1891 年 —— 苏联物理学家费德洛夫（ E.S.Fedorov ）发现了

十七种不同的铺嵌平面 的对称图案。

1924 年 —— 数学家波利亚（ Polya ）和尼格利（ Nigele ）

重新发现这个事实。

最有趣的是（ 1936 年）荷兰艺术家埃舍尔（ M.C.Escher ）

偶然到西班牙的格兰拿大旅行，在参观建于十四世纪的阿罕伯拉宫时，发现宫内的地板、天花板和墙壁满是密铺图案的装饰。因而得

到启发，创造了无数的艺术作品，给人留下深刻印象，更让人对数学有了新的认识。

扩展资料：

平面图形密铺的特点

1、用一种或几种全等图形进行拼接。

2、拼接处不留空隙、不重叠。

4、连续铺成一片。

能密铺的图形在一个拼接点处的特点

几个图形的内角拼接在一起时，其和等于

360º，并使相等的边互相重合。

参考资料来源：搜狗百科——密铺